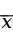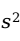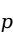总体参数虽然是未知的，但可以利用样本信息来推断。例如，我们从上述研究地区随机抽取400人组成一个样本，根据这400人的平均收入推断该地区所有人口的平均收入。这里400人的平均收入就是一个统计量（statistic），它是根据样本数据计算的用于推断总体的某些量，是对样本特征的某个概括性度量。因此，统计量是不含任何未知参数的样本的函数。由于样本是从总体中随机抽取的，样本具有随机性，由样本数据计算出的统计量也是随机的。所以理论上在抽样中，统计量是一个随机变量。

 

由样本统计量这个随机变量所形成的概率分布就是抽样分布（sampling distribution），即抽样分布就是统计量的分布，如样本均值的分布，样本比例的分布等。但当样本抽取出来以后，样本值就是已经观察到的值，这个样本的统计量就是已知的某个确定的值，是随机变量的一次实现值。

 

样本统计量可以看做是样本的函数，并且构成样本统计量的函数中不能包含未知参数。就一个样本而言，我们关心的统计量通常有样本均值（）、样本方差（）、样本比例（）等。应该注意到，不同的样本可以计算出不同的统计量值，一个总体能构成多少个不同的样本，就可以计算出多少个统计量的值，这些不同的统计量值就形成了理论上的抽样分布。现实生活中我们不可能把所有的样本都抽取一遍，所以，我们可以观察到一个样本的统计量值，但不能观察到所有可能的统计量值。因此，抽样分布仅仅是一种理论分布。既然统计量的取值是依据样本而变化的，那么，根据统计量来推断总体参数就必然具有某种不确定性。幸运的是，我们可以给出这种推断的可靠性，而度量这种可靠性的依据正是统计量的抽样分布，并且我们确知这种分布的某些性质。因此，统计量的抽样分布提供了该统计量长远而稳定的信息，它构成了推断总体参数的理论基础。